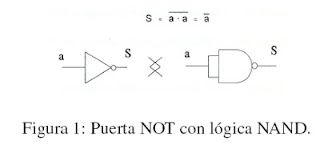
Aplicaciones de los circuitos combinacionales en la vida cotidiana

Los circuitos combinacionales se utilizan para operaciones lógicas y sólo tienen dos salidas. No pueden accionar directamente ningún tipo de carga, como los LED o los motores. Sin embargo, pueden integrarse con otros tipos de circuitos para accionar una carga final. La lógica combinacional es de naturaleza digital y utiliza señales cortas altas/bajas para representar verdadero o falso. Se utiliza en el cálculo de señales digitales como 0s y 1s. Las versiones más sencillas de estos circuitos existen desde el año 1700, pero las versiones electrónicas modernas son dispositivos muy sofisticados que sirven de base a todos los procesadores informáticos actuales. ¿ Cómo utilizas los circuitos combinacionales en tu vida ? Sigue leyendo para descubrirlo. Contadores electrónicos Una de las primeras aplicaciones de los circuitos combinacionales fue el diseño de contadores electrónicos. Estos dispositivos miden la cantidad de corriente que circula por un cable y proporcionan u...